Semana #37
Tema: Promedio aritmético
Media aritmética:
La media aritmética es la suma de todos los datos dividida entre el número total de datos. Se calculan dependiendo de cómo vengan ordenados los datos.
Ejemplo:
¿Cuál es la media de las edades de Andrea y sus primos?

Así, la media de las edades de Andrea y sus amigos:
Media =3+5+6+8+9+9+97=49
_______________ __ = 7
7 7
La media de edad es de 7 años.
Semana #36
Tema: Suma y resta de fracciones homogéneas

Semana # 33 a la 35
Tema: División de decimales
INICIA EL CUARTO PERIODO
Semana # 29
Tema: La potenciación

Semana # 26
Tema: Fracciones decimales y porcentaje
Transformación de decimal a fracción
Para escribir un número decimal en forma de fracción decimal, se escribe en el numerador el número decimal sin coma, y en el denominador la unidad seguida de tantos ceros como cifras decimales tiene el número decimal. La fracción obtenida se puede simplificar si lo deseas.
Por ejemplo:
Transformación de fracción decimal a número decimal
Una fracción decimal es aquella que tiene por denominador la unidad seguida de ceros: 10, 100, 100...
Ejemplo
Para escribir un fracción decimal en forma de número decimal, se escribe el numerador y se separan con una coma, hacia la derecha, tantas cifras decimales como ceros tenga el denominador. si es necesario se añaden ceros.
Ejemplo:
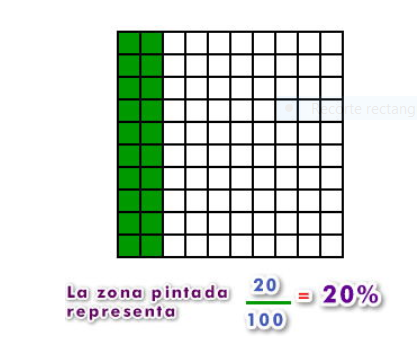
Las fracciones que tienen como denominador 100 se llaman porcentajes o tantos por ciento.
El porcentaje es denotado utilizando el signo porcentaje %, que se debe escribir inmediatamente después del número al que se refiere, sin dejar espacio de separación. Por ejemplo: "treinta y tres por ciento" se representa mediante 33% y significa "treinta y tres de cada cien".
Por ejemplo:
Al expresarse como porcentaje es posible comparar diferentes cantidades en relación a un todo que es 100.
Por ejemplo:
Cálculo de porcentajes
Para calcular el porcentaje de una cantidad se multiplica el número del porcentaje por la cantidad y se divide por cien.
Veamos un ejemplo dónde calcularemos el porcentaje de un número:
El cálculo de porcentajes nos pueden servir para múltiples aplicaciones, como por ejemplo problemas de comercio, geometría, encuestas de opinión, medición de índices de producción, natalidad, mortalidad, etc.
Descuento= 30% de 4 000 = (30 x 4 000) : 100 = 120.000 : 100 = 1200 pesos.
4000 – 1200 = 2800 pesos debe pagar.
Respuesta: José debe pagar $2800 por su pantalón.
Semana # 25
Tema: Fracción de un numero
Semana # 24
Tema: El metro cubico.
El metro cúbico (símbolo m³) es un unidad de medida de volumen. Es la unidad de volumen del Sistema Internacional de Unidades. Representa el volumen ocupado por un cubo de un metro de lado o arista. Equivale a un kilolitro (1000 litros).



Semana # 19
Tema: El litro y sus multiplos

Semana # 17
Tema: Clasificación de los triángulos
Según la medida de sus lados, los triángulos se pueden clasificar en:
- Equilatero
- Isósceles
- Escaleno
Triángulo Equilátero: Es aquel que tiene todos sus lados de la misma medida.
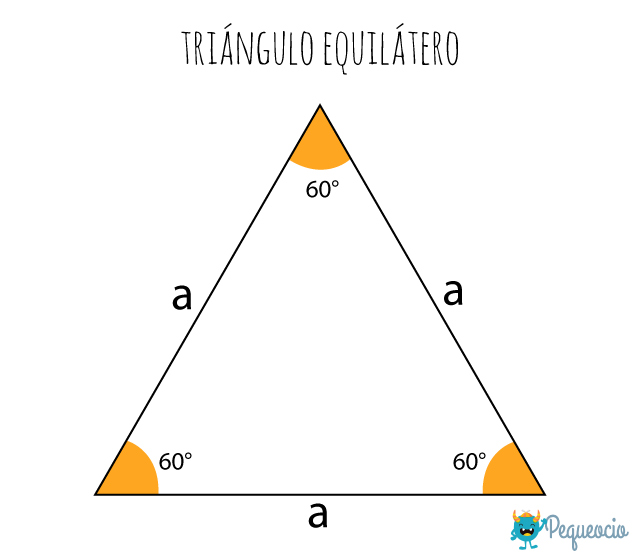
Triángulo Isósceles: Es aquel que tiene sólo dos lados de igual medida.

Triángulo Escaleno: Es aquel que tiene todos sus lados de distinta medida.

Clasificación de triángulos según la medida de sus ángulos
Según la medida de sus ángulos, los triángulos se pueden clasificar en:
- Acutángulo
- Rectángulo
- Obtusángulo
Triángulo Acutángulo: Aquel que tiene todos sus ángulos agudos.

Triángulo Rectángulo: Aquel que tiene un ángulo recto (< CAB).

Triángulo Obtusángulo: Aquel que tiene un ángulo obtuso.


Semana # 16
Tema: Paralelismo y perpendicularidad
Paralelismo: En la geometría, el paralelismo es una relación que se establece entre cualquier variedad lineal de dimensión mayor o igual que 1 (rectas, planos, hiperplanos y demás). En el plano cartesiano dos rectas son paralelas si tienen la misma pendiente o son perpendiculares a uno de los ejes, por ejemplo la función constante.
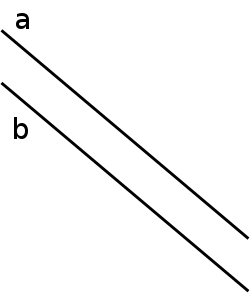
Perpendicularidad: En geometría, la condición de perpendicularidad, se da entre dos entes geométricos que se cortan formando un ángulo recto.
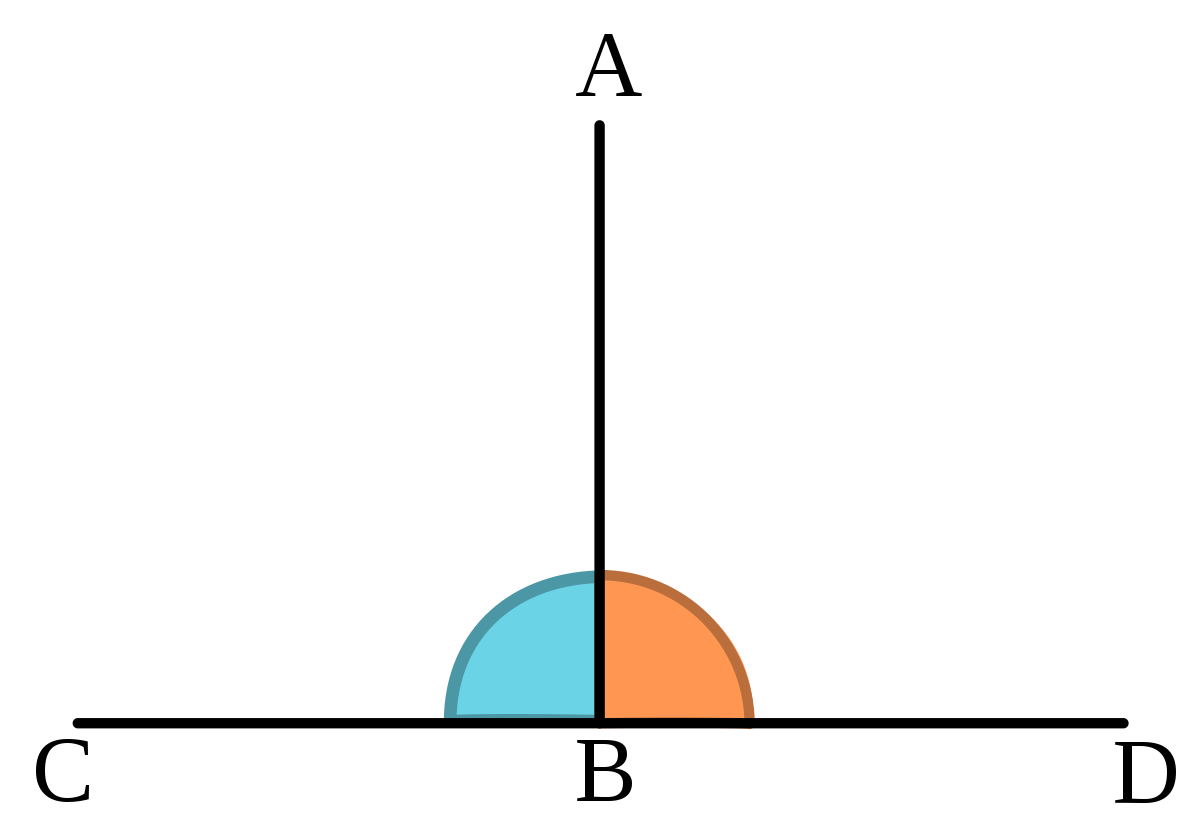
Tema: clasificación de polígonos
Los polígonos se clasifican según su forma, según el número de sus lados, y según da medida de sus lados y ángulos internos .
Los polígonos según la medida de sus de sus lados y ángulos interno se clasifican en Polígonos irregulares y Polígonos regulares:
POLÍGONO IRREGULAR: Se le llama polígono irregular a un polígono cuyos lados y ángulos interiores no son iguales entre sí. Los polígonos irregulares no tienen todos sus lados iguales. Sus vértices no están inscritos en una circunferencia. Estos polígonos irregulares tienen la ventaja de que no se necesita un compás para construirlos como es el caso de los polígonos regulares, sólo se necesita una regla para conectar los puntos para formar el polígono irregular con lados diferentes pero un punto no puede conectarse más de dos puntos porque sino se estaría formando dos polígonos juntos o continuos.
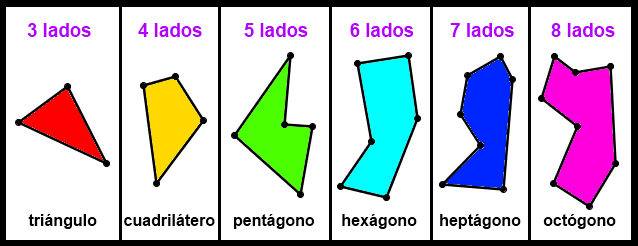
POLÍGONO REGULAR: Es un polígono en el cual todos sus lados y ángulos tienen la misma medida. Los polígonos regulares reciben un nombre especial según el número de sus lados.

Los cuadriláteros son polígonos de cuatro lados y la suma de sus ángulos interiores es igual a 360°.
Clasificación de cuadriláteros: Los cuadriláteros tienen tres clasificaciones principales: paralelogramos, trapecios y trapezoides.
Paralelogramos: Son los cuadriláteros que tienen los lados paralelos dos a dos.
Se clasifican en:
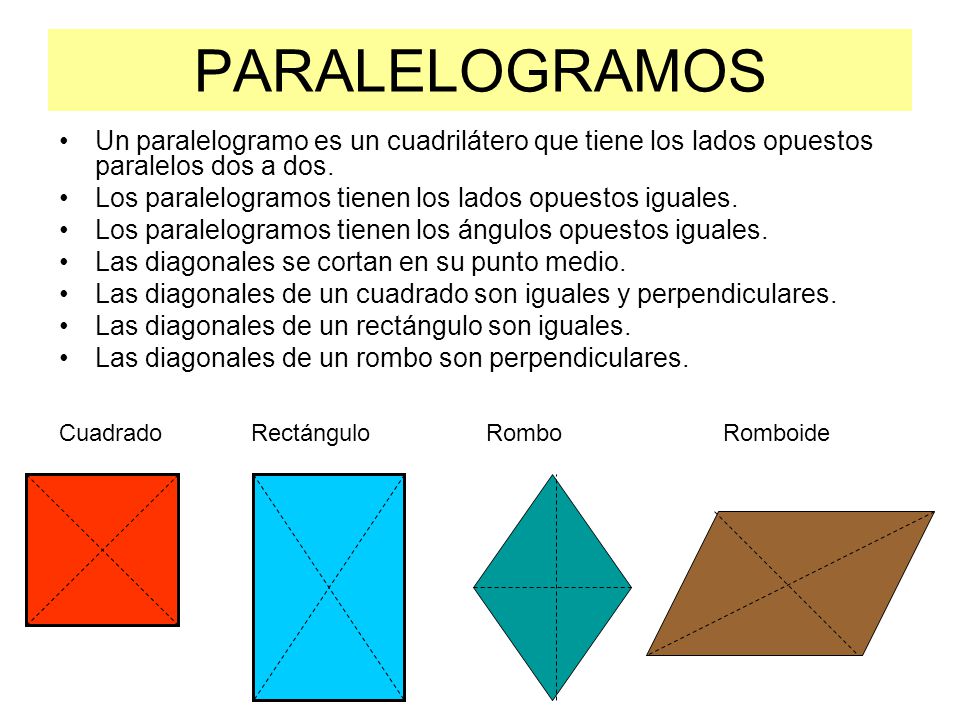
Trapecios: Cuadriláteros que tienen dos lados paralelos, llamados base mayor y base menor. Se clasifican en:

Semana # 14
Tema: el metro cuadrado
Un metro cuadrado, representado con el símbolo m², es el área dentro en un cuadrado cuyos lados miden un metro. Es la unidad básica de superficie en el Sistema Internacional de Unidades.
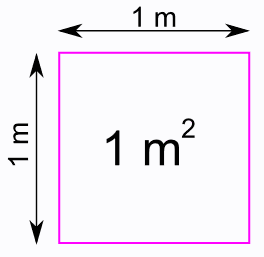
Si a esta unidad se antepone un prefijo del Sistema Internacional se crea un múltiplo o submúltiplo de esta. Sin embargo al presentarse al cuadrado, la diferencia de la orden de magnitud se eleva si se compara con las unidades lineales de igual prefijo. Por ejemplo, un kilómetro es mil veces la longitud de un metro, pero un kilómetro cuadrado es un millón de veces el área de un metro cuadrado.

Semana # 13
Tema: Miltiplos y submultiplos del metro
Medidas de longitud:
Corresponden a unidades de medida que sirven para saber cuán largo es un objeto. La unidad que se utiliza internacionalmente para medir longitudes, es el metro (m). De esta unidad provienen otras más pequeñas (llamadas submúltiplos) o más grandes (llamadas múltipos).
Equivalencias de longitud
A continuación se indican algunas unidades más pequeñas (submúltiplos) del metro, éstas son el decímetro (dm) y el centímetro (cm).


Semana # 12
Tema: Miltiplicación de decimales
INICIO DEL 2° PERIODO
Semana # 10
Tema: Realización de encuesta, organización de las respuestas, tabulación de datos y gratificación en diagrama de barras.
Imágenes del desarrollo de la actividad.
Semana # 04 y 05


Observemos el valor posicional según sus dígitos:

Actividad:
1. completar la tabla:
2. Realiza las sumas y colorea según las indicaciones:
Semana # 03
ACTIVIDAD:
Visualiza el vídeo y resuelve la actividad propuesta según la técnica presentada.
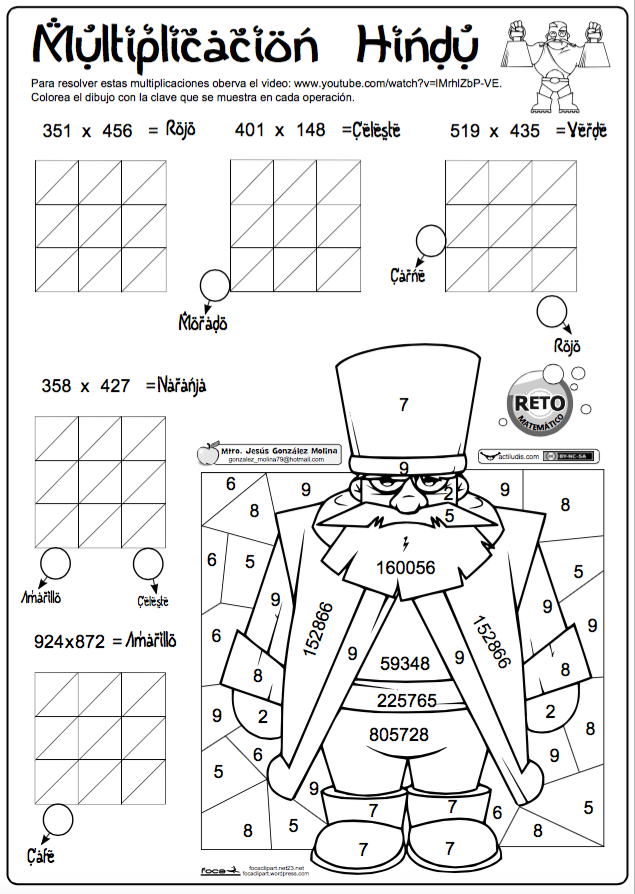
Semana # 02
Observa el vídeo y copia en tu cuaderno del área, los conceptos de los temas abordados.
Semana # 01

Tema: Promedio aritmético
Media aritmética:
La media aritmética es la suma de todos los datos dividida entre el número total de datos. Se calculan dependiendo de cómo vengan ordenados los datos.
Ejemplo:
¿Cuál es la media de las edades de Andrea y sus primos?

Así, la media de las edades de Andrea y sus amigos:
Media =3+5+6+8+9+9+97=49
_______________ __ = 7
7 7
La media de edad es de 7 años.
Semana #36
Tema: Suma y resta de fracciones homogéneas

Semana # 33 a la 35
Tema: División de decimales
INICIA EL CUARTO PERIODO
Semana # 29
Tema: La potenciación

Semana # 26
Tema: Fracciones decimales y porcentaje
Transformación de decimal a fracción
Para escribir un número decimal en forma de fracción decimal, se escribe en el numerador el número decimal sin coma, y en el denominador la unidad seguida de tantos ceros como cifras decimales tiene el número decimal. La fracción obtenida se puede simplificar si lo deseas.
Por ejemplo:
Transformación de fracción decimal a número decimal
Una fracción decimal es aquella que tiene por denominador la unidad seguida de ceros: 10, 100, 100...
Ejemplo
Para escribir un fracción decimal en forma de número decimal, se escribe el numerador y se separan con una coma, hacia la derecha, tantas cifras decimales como ceros tenga el denominador. si es necesario se añaden ceros.
Ejemplo:
Fracciones y porcentajes
Las fracciones que tienen como denominador 100 se llaman porcentajes o tantos por ciento.
El porcentaje es denotado utilizando el signo porcentaje %, que se debe escribir inmediatamente después del número al que se refiere, sin dejar espacio de separación. Por ejemplo: "treinta y tres por ciento" se representa mediante 33% y significa "treinta y tres de cada cien".
Por ejemplo:
Al expresarse como porcentaje es posible comparar diferentes cantidades en relación a un todo que es 100.
Por ejemplo:
Cálculo de porcentajes
Para calcular el porcentaje de una cantidad se multiplica el número del porcentaje por la cantidad y se divide por cien.
Veamos un ejemplo dónde calcularemos el porcentaje de un número:
El cálculo de porcentajes nos pueden servir para múltiples aplicaciones, como por ejemplo problemas de comercio, geometría, encuestas de opinión, medición de índices de producción, natalidad, mortalidad, etc.
Descuento= 30% de 4 000 = (30 x 4 000) : 100 = 120.000 : 100 = 1200 pesos.
4000 – 1200 = 2800 pesos debe pagar.
Respuesta: José debe pagar $2800 por su pantalón.
Semana # 25
Tema: Fracción de un numero
Semana # 24
Tema: El metro cubico.
El metro cúbico (símbolo m³) es un unidad de medida de volumen. Es la unidad de volumen del Sistema Internacional de Unidades. Representa el volumen ocupado por un cubo de un metro de lado o arista. Equivale a un kilolitro (1000 litros).

Semana # 19
Tema: El litro y sus multiplos
La capacidad mide la cantidad de líquido que cabe dentro de un objeto. Por ejemplo, la capacidad de una botella es la cantidad de líquido con la que podemos llenarla. Otra forma de llamar a la capacidad es volumen. Digamos que la capacidad es el volumen que ocupa un cuerpo en el espacio.
La unidad principal para medir la capacidad de un objeto es el litro. Pero no es la única que tenemos. Están los múltiplos, que son las unidades para expresas capacidades más grandes que el litro y los submúltiplos, que son las unidades para expresas capacidades más pequeñas.
Podemos ver las unidades de capacidad en la siguiente tabla:

Semana # 17
Tema: Clasificación de los triángulos
Clasificación de triángulos según la medida de sus lados.
- Equilatero
- Isósceles
- Escaleno
Triángulo Equilátero: Es aquel que tiene todos sus lados de la misma medida.

Triángulo Isósceles: Es aquel que tiene sólo dos lados de igual medida.

Triángulo Escaleno: Es aquel que tiene todos sus lados de distinta medida.

Clasificación de triángulos según la medida de sus ángulos
Según la medida de sus ángulos, los triángulos se pueden clasificar en:
- Acutángulo
- Rectángulo
- Obtusángulo
Triángulo Acutángulo: Aquel que tiene todos sus ángulos agudos.

Triángulo Rectángulo: Aquel que tiene un ángulo recto (< CAB).

Triángulo Obtusángulo: Aquel que tiene un ángulo obtuso.

Semana # 16
Tema: Paralelismo y perpendicularidad
Paralelismo: En la geometría, el paralelismo es una relación que se establece entre cualquier variedad lineal de dimensión mayor o igual que 1 (rectas, planos, hiperplanos y demás). En el plano cartesiano dos rectas son paralelas si tienen la misma pendiente o son perpendiculares a uno de los ejes, por ejemplo la función constante.

Perpendicularidad: En geometría, la condición de perpendicularidad, se da entre dos entes geométricos que se cortan formando un ángulo recto.
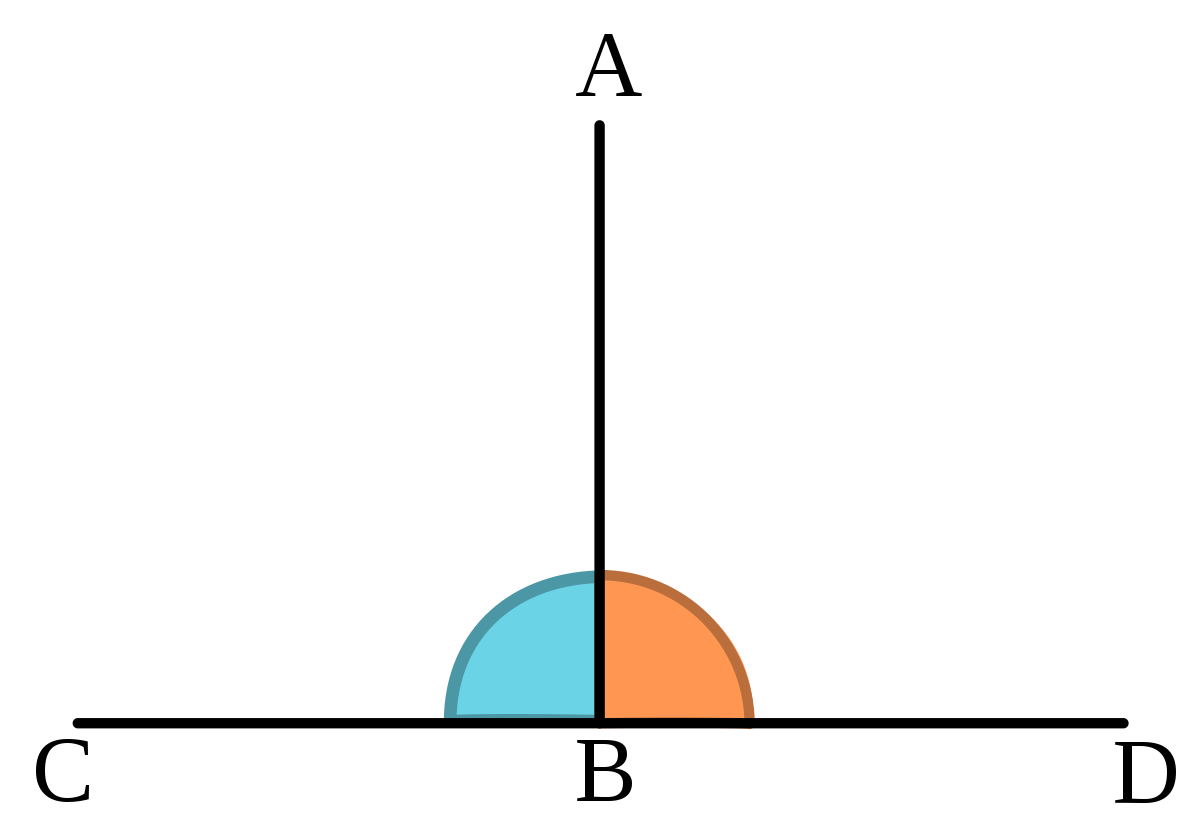
Tema: clasificación de polígonos
Los polígonos se clasifican según su forma, según el número de sus lados, y según da medida de sus lados y ángulos internos .
Los polígonos según la medida de sus de sus lados y ángulos interno se clasifican en Polígonos irregulares y Polígonos regulares:
POLÍGONO IRREGULAR: Se le llama polígono irregular a un polígono cuyos lados y ángulos interiores no son iguales entre sí. Los polígonos irregulares no tienen todos sus lados iguales. Sus vértices no están inscritos en una circunferencia. Estos polígonos irregulares tienen la ventaja de que no se necesita un compás para construirlos como es el caso de los polígonos regulares, sólo se necesita una regla para conectar los puntos para formar el polígono irregular con lados diferentes pero un punto no puede conectarse más de dos puntos porque sino se estaría formando dos polígonos juntos o continuos.

POLÍGONO REGULAR: Es un polígono en el cual todos sus lados y ángulos tienen la misma medida. Los polígonos regulares reciben un nombre especial según el número de sus lados.
¿Qué son los cuadriláteros?
Los cuadriláteros son polígonos de cuatro lados y la suma de sus ángulos interiores es igual a 360°.
Clasificación de cuadriláteros: Los cuadriláteros tienen tres clasificaciones principales: paralelogramos, trapecios y trapezoides.
Paralelogramos: Son los cuadriláteros que tienen los lados paralelos dos a dos.
Se clasifican en:

Trapecios: Cuadriláteros que tienen dos lados paralelos, llamados base mayor y base menor. Se clasifican en:

Semana # 14
Tema: el metro cuadrado
Un metro cuadrado, representado con el símbolo m², es el área dentro en un cuadrado cuyos lados miden un metro. Es la unidad básica de superficie en el Sistema Internacional de Unidades.

Si a esta unidad se antepone un prefijo del Sistema Internacional se crea un múltiplo o submúltiplo de esta. Sin embargo al presentarse al cuadrado, la diferencia de la orden de magnitud se eleva si se compara con las unidades lineales de igual prefijo. Por ejemplo, un kilómetro es mil veces la longitud de un metro, pero un kilómetro cuadrado es un millón de veces el área de un metro cuadrado.
Semana # 13
Tema: Miltiplos y submultiplos del metro
Medidas de longitud:
Corresponden a unidades de medida que sirven para saber cuán largo es un objeto. La unidad que se utiliza internacionalmente para medir longitudes, es el metro (m). De esta unidad provienen otras más pequeñas (llamadas submúltiplos) o más grandes (llamadas múltipos).
Equivalencias de longitud
A continuación se indican algunas unidades más pequeñas (submúltiplos) del metro, éstas son el decímetro (dm) y el centímetro (cm).
Semana # 12
Tema: Miltiplicación de decimales
INICIO DEL 2° PERIODO
Semana # 10
Tema: Realización de encuesta, organización de las respuestas, tabulación de datos y gratificación en diagrama de barras.
Imágenes del desarrollo de la actividad.
Semana # 04 y 05
LOS NÚMEROS DECIMALES
Los números decimales son valores que denotan números racionales e irracionales, es decir que los números decimales son la expresión de números no enteros, que a diferencia de los números fraccionarios, no se escriben como el cociente de dos números enteros sino como una aproximación de tal valor.
Lectura de números decimales:
Recuerda que un número decimal tiene dos partes: la parte entera, a la izquierda de la coma, y la parte decimal, a la derecha de la coma. Para leer y escribir un número decimal, primero se considera la parte entera y luego la decimal, indicando los décimos o centésimos, según corresponda.
6,8 ⇒ Se lee, Seis enteros ocho décimos o seis coma ocho
4,11 ⇒ Se lee, Cuatro enteros once centésimas o cuatro coma once

Observemos el valor posicional según sus dígitos:

Actividad:
1. completar la tabla:
2. Realiza las sumas y colorea según las indicaciones:
Semana # 03
ACTIVIDAD:
Visualiza el vídeo y resuelve la actividad propuesta según la técnica presentada.

Semana # 02
Observa el vídeo y copia en tu cuaderno del área, los conceptos de los temas abordados.
Semana # 01
Historia de las matemáticas
Ingresa al siguiente enlace y visualiza la verdadera historia de las matemáticas.
EL SISTEMA DE NUMERACIÓN
Nuestro sistema de numeración tiene dos características esenciales: es decimal y es posicional.
Es decimal porque; utilizamos 10 dígitos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9
Agrupamos de 10 en 10 en órdenes cada vez mayores:
10 U = 1 D
10 D = 1 C
10 C = 1 UM
10 UM = 1 DM
Se representan así:
Es posicional porque el valor de cada cifra en un número depende del lugar que ocupa.
En el número 370.241 la cifra 2 ocupa el orden de las centenas, por lo tanto 2C = 20D = 200U
La cifra 7 ocupa el orden de las decenas de millar, por lo tanto 7DM = 70UM = 700C = 7.000D = 70.000U


































pues haciendo una tarea :v
ResponderEliminarHola profe
ResponderEliminarhola estudiante
ResponderEliminarque
EliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarHola profe
ResponderEliminar